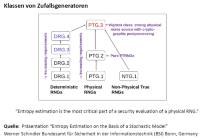
Welche Anforderungen werden an kryptografisch sichere Zufallsgeneratoren gestellt?

Für die Erzeugung und Bewertung von kryptografisch sicheren Zufallszahlen sind eindeutige Normen und Vorschriften vorgegeben. Diese sind neben dem Algorithmenkatalog der Bundesnetzagentur in den AIS31-Dokumenten des Bundesamtes für Sicherheit in der Informationstechnik (BSI) festgelegt und bestimmen die notwendigen Eigenschaften von unbearbeiteten Zufallszahlen (Rohdaten): „Funktionalitätsklassen und Evaluationsmethodologie für physikalische Zufallszahlengeneratoren“

Demnach muss ein kryptografisch sicherer Zufallsgenerator z.B. eine Entropie der Zufalls-Rohdaten von mehr als 7,97 Bit/Byte haben. Weiterhin müssen die Zufallsbits bestimmten Eigenschaften genügen, wie die Gleichverteilung, Bitunabhängigkeit und die Bewertung von 2-, 3-, und 4-Bit Zufallsfolgen.

Grundsätzlich verlangt die Bundesnetzagentur im aktuellen Algorithmenkatalog 2016 :

„Für Zertifizierungsdienstanbieter wird die Verwendung von Zufallsgeneratoren der Funktionalitätsklassen PTG.3 und DRG.4 im Grundsatz ab 2016 verpflichtend werden, sowohl allgemein bei der Erzeugung von Langzeitschlüsseln als auch bei der Erzeugung von Ephemeralschlüsseln.

Bemerkungen:

• Hybride Zufallszahlengeneratoren vereinen Sicherheitseigenschaften von deterministischen und physikalischen Zufallszahlengeneratoren.

• Hybride physikalische Zufallszahlengeneratoren der Klasse PTG.3 besitzen neben einer starken Rauschquelle eine starke kryptographische Nachbearbeitung mit Gedächtnis.

• PTG.3 stellt die stärkste Funktionalitätsklasse dar.“

Zahlreiche Meldungen kritisieren Lücken, Schwächen und Manipulationen bei der Erzeugung von Zufallszahlen für kryptografische Verfahren. Eine Sammlung verschiedener Quellen finden Sie in dieser unvollständigen Sammlung von Pressemeldungen. Daher wird generell für die Generierung von kryptografisch sicheren Zufallszahlen empfohlen, keine Lösung zu verwenden, die auf der Basis von Closed-Source-Hardware aus dem nichteuropäischen Ausland arbeitet oder auf den von der Computer Security Division am NIST der USA für den praktischen Einsatz empfohlenen Zufallserzeugungen beruht.

Halbleiterrauschen als Entropie-Quelle

Die in den Zufallsgeneratoren des IBB verwendeten Rauschquellen sind Halbleiter-Bauelemente mit Signalamplituden von >50mV und Frequenzbereichen bis 50MHz. Diese ausgewählten Standard-Bauteile müssen nicht ausgemessen werden und besitzen, technologisch bedingt, alle gleiche nichtspezifizierte Eigenschaften.

Unter Rauschen versteht die Physik allgemein eine Störgröße mit breitem unspezifischem Frequenzspektrum. Es kann daher als eine Überlagerung vieler harmonischer Schwingungen oder Wellen mit unterschiedlicher Amplitude und Frequenz beziehungsweise Wellenlänge interpretiert werden. Rauschen wurde als physikalisches Phänomen, nämlich als messbare unregelmäßige Stromschwankungen, erstmals 1918 durch Walter Schottky beschrieben. Der Strom durch einen in Sperrrichtung gepolten Halbleiter ist durch den Diffusionsstrom von Minoritätsladungsträgern am Rand der Raumladungszone und durch den Generationsstrom aus der Raumladungszone bestimmt. In beiden Fällen erzeugt die Drift der Ladungsträger in der Raumladungszone eine Kette von näherungsweise unabhängigen Strompulsen, deren Mittelwert den Gleichstrom und deren Schwankungen Rauschen bewirkt. Das mit der Diffusion von Ladungsträgern in die Raumladungszone (pn-Übergang) hinein verknüpfte Rauschen sei mit “Diffusions-Rauschen“, das mit der Generation von Ladungsträgern in der Raumladungszone verknüpfte Rauschen als “Generations-Rauschen“ bezeichnet. (https://de.wikipedia.org/wiki/Rauschen_(Physik))

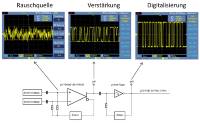
Patentiertes Blockschaltbild und Messsignale

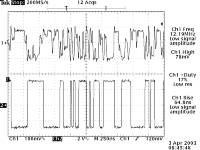
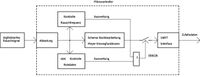
Die Rauschsignale zweier Z-Dioden werden einem Differenzverstärker zugeführt, der eine ca. 300-fache Verstärkung realisiert und durch die hohe Gleichtaktunterdrückung Störsignale sehr wirksam eliminiert. Ein schneller Schmitt-Trigger digitalisiert das verstärkte Rauschsignal und führt es einem Porteingang des Mikrocontrollers zu. Die Rückkopplung mittels Tiefpass garantiert einen stabilen Arbeitspunkt der Verstärkung und Digitalisierung. Entscheidend für eine hohe und robuste Entropie und damit einer hohen Gleichverteilung der nach der Digitalisierung verwendeten logischen Signale (0,1) ist eine hohe virtuelle Symmetrie in allen Signalwegen.

Entropie

Unter Entropie versteht man in der Informationstechnik die Unvorhersagbarkeit der Information. Das informationstheoretische Verständnis des Begriffes Entropie geht auf Claude E. Shannon zurück und existiert seit etwa 1948. In diesem Jahr veröffentlichte Shannon seine fundamentale Arbeit A Mathematical Theory of Communication und prägte damit die moderne Informationstheorie. Weitere Erläuterungen finden Sie hier.

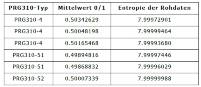
Auf Grund der sehr hohen Entropie der robusten Rauschquellen von >7,997 Bit/Byte wurden Funktionen verschiedener Applikationen für die Klassen PTG.2 und/oder PTG.3 entwickelt. Kein bekannter kommerzieller Zufallsgenerator weltweit erreicht die hohen Entropiewerte der IBB-Applikationen. Voraussetzung für die Berechnung der Entropie (z.B. nach Shannon) ist die Generierung von Zufalls-Rohdaten. Jede weitere mathematisch-kryptografische Bearbeitung kann die Entropie nicht weiter erhöhen! Die Tabelle rechts zeigt reproduzierbare Entropiewerte des PRG310.

Physikalisch-stochastisches Modell

Grundlage der im Folgenden vorgestellten Lösungen zur Klasse PTG.3 ist ein physikalisch-stochastisches Modell, mit dem die Leistungsfähigkeit zur Generierung kryptografisch sicherer Zufallszahlen begründet wird. Dieses Modell erklärt:

die robuste und hohe Entropie der Rauschquelle
das Prinzip der Abtastung des digitalisierten Rauschsignals
die permanente Überwachung der Rauschquelle durch Frequenzmessung
die kryptografische Nachbearbeitung durch Meyer-Einwegfunktionen (Schema)
den permanenten statistischen Online-Test der Zufalls-Rohdaten

Hybride Zufallszahlengeneratoren der Klasse PTG.3

Hybride Zufallszahlengeneratoren vereinen Sicherheitseigenschaften von deterministischen und physikalischen Zufallszahlen-generatoren und besitzen neben einer starken Rauschquelle eine starke kryptographische Nachbearbeitung mit Gedächtnis. Die Klasse PTG.3 stellt nach Algorithmenkatalog 2016 der Bundesnetzagentur (BNetzA) die stärkste Funktionalitätsklasse dar.

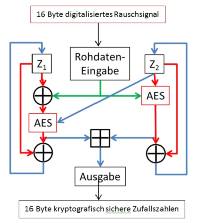
Diese kryptografische Nachbereitung nutzt 2 Prinzipien des Entropiesammelns: das Aufxorieren der Rohdaten für z1 und die Glättung durch Aufxorieren des mit zufälligem Schlüssel verschlüsselten Zustands für z2. Beide Komponenten nutzen die Meyer-Einwegfunktion AES(k,s) xor k um den vorangegangenen inneren Zustand zu schützen. Durch die XOR-Summe der Zwischenwerte kann nicht auf den inneren Zustand geschlossen werden. Wenn die Addition mod 256 durch XOR ersetz würde, würde für bekannte Ausgabe o i und Folgezustand z i+1 gelten, d.h. aus dem bekannten Zustand und vorhergehenden Ausgaben kann die Xor-Summe beider Teile berechnet werden. Dadurch werden auch bei einem kurzzeitigen Ausfall oder Manipulation der Rauschquellen statistisch gleichverteilte Zufallsdaten ausgegeben

Die Zufalls-Rohdaten-Eingabe erfolgt mit 16 Byte digitalisierter Rauschdaten des physikalischen Zufallsgenerators und ergeben nach der Verarbeitung 16 Byte kryptografisch sichere Zufallszahlen. Es wird also explizit kein Pseudozufall generiert.

Statistische Analysen

Zahlreiche statistische Untersuchen mit allen Zufallsgeneratoren bestätigen Eigenschaften, die einem idealen Zufallszahlengenerator sehr nahe kommen. Zur Evaluierung wurden umfangreiche statistische Tests durchgeführt. Bereits die Untersuchung der Zufalls-Rohdaten zeigte eine sehr hohe Entropie und keine nachweisbaren Abhängigkeiten der Zufallsbits. Die mit empfohlenen Methoden nach Schema der Klasse PTG.3 nachbearbeiteten Zufallsdaten wurden mit internationalen Referenztests, wie der Diehard-Test-Suite nach George Marsaglia, der NIST-Test-Suite und einem weiteren eigenen statistischen Basistest, umfangreich untersucht. Keine der generierten Testfolgen konnte Unterschiede zu den Ergebnissen eines idealen Zufallszahlengenerators aufzeigen. Für jeden angebotenen Zufallsgenerator stehen diverse statistische Analysen, auch im erweiterten Temperaturbereich, zur Verfügung.

Beispiele verwendeter statistischer Analysen